NEW!第77回 午前 94

画像工学

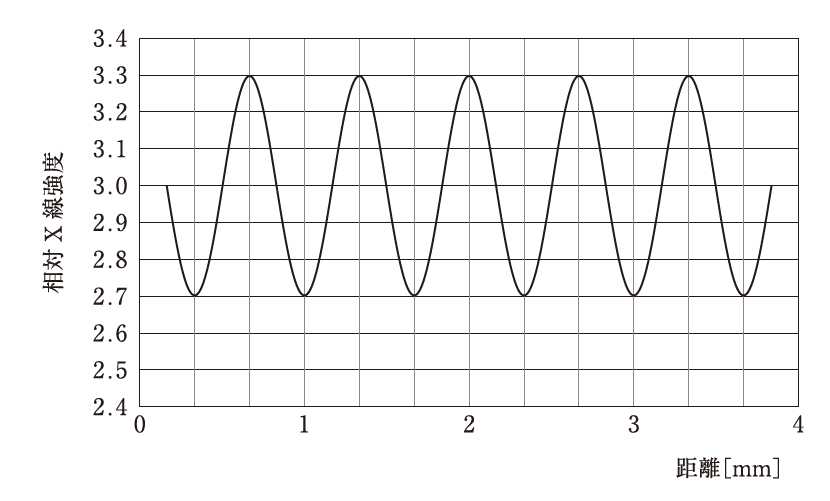
図のような周期パターンのMichelson〈マイケルソン〉コントラストはどれか。

  1. 0.1
  2. 0.6
  3. 0.2
  4. 0.7
  5. 0.3

出典：厚生労働省公開PDF（令和7年版）

1． 0.1

解説

✔　Michelson〈マイケルソン〉コントラストとは？

Michelsonコントラストは、CTやMRIで解像度を評価する際に用いるバーチャートのような、周期的（波や縞模様）なパターンのコントラストを定量的に評価するための指標です。

「最も明るい部分」と「最も暗い部分」の輝度（または信号強度）の差を、それらの和（全体の明るさ）で割ることで、全体の明るさに対する明暗の相対的な度合いを算出します。

✔　計算方法

計算式は以下の通りです。

C=（Imax​－Imin）​/（ Imax​＋Imin）​​

  • C: Michelsonコントラスト
  • Imax: 輝度の最大値（波の山の高さ）
  • Imin: 輝度の最小値（波の谷の深さ）

問題に示されたグラフから、これらの値を読み取って計算します。

  1. グラフから最大値と最小値を読み取る
    • Imax ≈ 3.3
    • Imin ≈ 2.7
  2. 公式に代入して計算する
    • C= (3.3－2.7) / (3.3＋2.7​) =0.6/6.0​=0.1

したがって、正解は 1. の 0.1 となります。

出題者の“声”

この問題は、画像評価の基本である「コントラスト」の計算式を、正しく知っておるかを問う、非常にシンプルな計算問題じゃ。ひねりも何もない、知識と計算の正確さだけが試される。

ワナがあるとすれば、２つじゃな。

1つは、Michelsonコントラストの公式を知らんこと。これでは手も足も出ん。

もう1つは、Weberコントラストのような、別のコントラストの定義と混同することじゃ。

（最大－最小）÷ 最小ではないぞ。分母は（最大＋最小）じゃ。

「周期的なパターンにはMichelsonコントラスト」と、条件と公式をセットで覚えておれば、これは確実に得点できるサービス問題じゃよ。

臨床の“目”で読む

私たちが日常業務でMichelsonコントラストを直接計算する場面はほとんどありません。しかし、この計算は、私たちが使う画像診断装置性能を評価する上で、最も重要な指標である「MTF」と深く関わっています。

ーMTF（変調伝達関数）との関係ー

MTF (Modulation Transfer Function)は、その画像診断装置が、被写体の持つコントラストをどれだけ忠実に画像上で再現できるかを示す、「解像性能（鮮鋭度）」の指標です。

MTFを測定する際には、濃淡の縞模様が描かれた「バーチャート（テストファントム）」を撮影します。そして、元々のファントムが持つコントラスト（入力コントラスト）と、撮影された画像上の縞模様のコントラスト（出力コントラスト）を、まさにこのMichelsonコントラストの式を使って計算するのです。

MTF = （出力コントラスト） / （入力コントラスト）

このMTFの値が高いほど、その装置は微細な構造まで鮮明に描き出せる「高性能な装置」であると言えます。

つまり、この一見単純なコントラスト計算は、CTやマンモグラフィといった装置の根本的な性能を決定づける、極めて重要な物理評価の基礎となっているのです。

今日のまとめ

  1. 周期的なパターンのコントラストを評価するMichelsonコントラストの公式は、C=（Imax​－Imin）​/（ Imax​＋Imin）​​
  2. 計算手順は、①グラフから最大値(Imax)と最小値(Imin)を読み取り、②公式に代入する。
  3. この計算は、画像の鮮鋭度を評価する最重要指標であるMTF（Modulation Transfer Function）の測定に応用されている。
  4. 分母が「最大値と最小値の和」であることを、他のコントラスト定義と混同しないよう注意する。

コメント