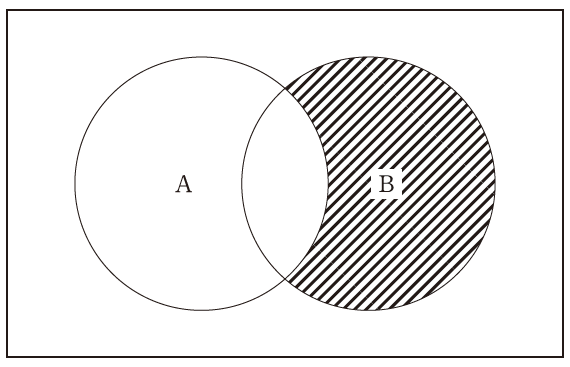
集合A、Bからなるベン図で斜線部分を表すのはどれか。
- NOT A
- A XOR B
- A NAND B
- NOT (A XOR B)
- (NOT A) AND B
出典:厚生労働省公開PDF(令和7年版)
5. (NOT A) AND B
解説
✔ ベン図を「言葉」と「論理式」に翻訳する ✍️
この問題を解く鍵は、図で示された領域をまず「言葉」で定義し、それを「論理式」に変換することです。
Step 1:図を言葉で表現する
図の斜線部分は、「集合Bに属している」かつ「集合Aには属していない」領域です。
これを一言で言えば「Bだけの部分」となります。
Step 2:言葉を論理式に変換する
次に、Step 1の言葉を論理演算子に置き換えます。
「集合Bに属している」 → B
「集合Aには属していない」 → NOT A
「かつ」 → AND
これらを組み合わせると、斜線部分を表す論理式は (NOT A) AND Bとなります。
✔ 基本的な論理演算子

✔ 各選択肢について
1. NOT A
- ❌ 誤り
- Aの円の外側すべてを指します。
2.A XOR B
- ❌ 誤り
- 「Aだけの部分」と「Bだけの部分」の両方を合わせた領域を指します。
3.A NAND B
- ❌ 誤り
- AとBの共通部分以外のすべてを指します。
4.NOT (A XOR B)
- ❌ 誤り
- 「AとBの共通部分」と「AとBのどちらでもない外側の部分」の両方を合わせた領域を指します。
5. (NOT A) AND B
- ✅ 正解
- 解説の通り、「Aではなく、かつBである」部分、つまり「Bだけの部分」を正確に示しています。
出題者の“声”

この問題の狙いは、ベン図で示された差集合の領域を、論理式の組み合わせで正しく表現できるか、という基本を問うことにある。
図を言葉に直せば「Bだけ」、それを論理式に翻訳すれば「B AND (NOT A)」。この思考の流れがスムーズにできるかが勝負じゃ。
学生が最もひっかかりやすいのが、2番のXOR。XORは「Aだけ」と「Bだけ」の両方を含む。図が片方の領域しか塗られていない点を見落とすと、このワナにはまる。
集合の図、言葉、そして論理式の3つを、頭の中で自在に行き来できる訓練をしておくことが重要じゃ。
臨床の“目”で読む

ー画像処理におけるマスク演算ー
この集合演算の考え方は、医療画像の解析、特にマスク処理において日常的に使われています。
例えば、
- B = 「肝臓全体の関心領域(ROI)」
- A = 「肝臓内の、評価対象外としたい血管領域」
- このとき、「肝臓の実質部分だけ」の情報を抽出したい場合、まさに (NOT A) AND B 、すなわち「肝臓全体から、血管領域を除く」という演算が行われます。
これは、特定の臓器の体積測定、病変の個数カウント、線量分布評価における特定領域の線量集計など、あらゆる画像解析の基礎となる極めて実用的な技術なのです。
今日のまとめ
- 図の斜線部分が示すのは「Bだけの部分」であり、論理式では (NOT A) AND B と表現される。
- XORは「Aだけ」と「Bだけ」の両方を含むため、片側だけの図とは異なる点に注意。
- 集合演算の考え方は、ROI抽出などの画像マスク処理に応用される実践的な知識である。




コメント