第77回 午後 94

焦点検出器間距離を100 cmから120 cmに変え、その他の条件を同一としてX線撮影を実施した。
受像面のX線量の倍数で最も近い値はどれか。

出典：厚生労働省公開PDF（令和7年版）

✅ 正解を表示

1．0.69

解説

この問題は、放射線物理学の絶対ルール、「逆二乗則」を使った計算問題です。公式を覚える前に、まずは懐中電灯をイメージしてください。

✔　イメージで解く：光は離れると“急激に”暗くなる 🔦

壁に懐中電灯を向けて、後ろに下がっていくと、光の輪は大きくなりますが、明るさは暗くなりますよね？ X線も同じです。

距離が伸びる（100cm → 120cm）
- → 線量は絶対に減る（1.0未満になる）。
- この時点で、増えている選択肢 3, 4, 5 は即座に消去できます。

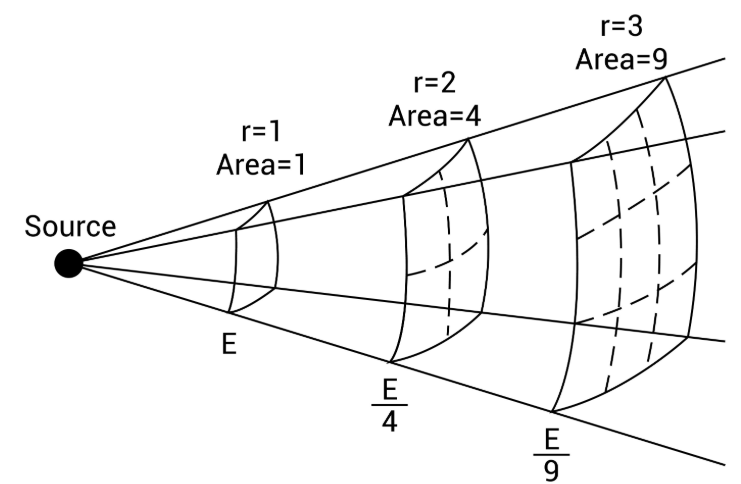
✔　計算テクニック：分数の「2乗」を恐れるな

線量の変化は、距離の比率の「2乗」に反比例します。新しい線量を求める式はこうです。

新しい線量 = （元の距離 / 新しい距離）²

今回の数字を当てはめます。　（100 / 120）²　→ここで、いきなり2乗せず、約分するのがコツです。

（5 / 6）² = 25/36 = 0.693

よって、正解は 0.69（選択肢1） です。

出題者の“声”

この問題の狙いは、「逆二乗則の計算ができるか」以上に、「物理的な直感を持っているか」を試しておる。

距離が 100cm から 120cm に伸びた。この瞬間、「線量は減るはずだ（答えは1より小さい）」と直感できないと、平気で 1.44 を選んでしまう。

計算する前に、「増えるか？減るか？」を予想する。これが計算ミスをなくす最強の検算じゃ。

臨床の“目”で読む

ーポータブル撮影で「写真がザラザラ！」失敗を防ぐー

病室でのポータブル撮影では、ベッドの配置などで毎回距離（SID）が変わります。普段 100cm で撮っている条件（mAs）のまま、うっかり 120cm の距離で撮影してしまったらどうなるでしょう？

この問題の通り、線量は 0.69倍（約7割）にまで落ち込みます。その結果、写真は「濃度不足（真っ白）」で、ノイズだらけの失敗写真になります。

この「距離補正」を瞬時にできるのが、技師の腕の見せ所です。

今日のまとめ

第77回午後 94