放射線源からの放射線を測定するとき、測定時間 t の全計数値を N とする。
標準偏差を含む計数率はどれか。
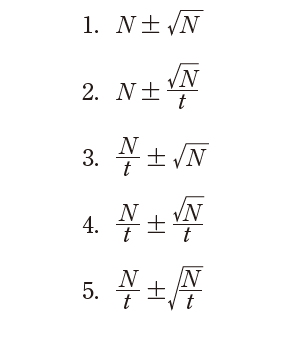
出典：厚生労働省公開PDF（令和7年版）
５
解説
この問題は、放射線測定の「不確かさ（ゆらぎ）」を、「全計数値」から「計数率」へ、正しく計算できますか？ という問題です。 数式にアレルギーを起こさず、以下のステップで考えてみましょう。
✔ すべての出発点：全計数値（N）の“ゆらぎ”
放射線は、ポツ…ポツ…とランダムに飛んできます（ポアソン分布）。 そのため、測定時間 t で、たまたま N 回カウントできたとしても、この N という値は、測定のたびに必ずゆらぎます。
そして、この「ゆらぎ」の大きさ（＝標準偏差）には、鉄板のルールがあります。
「N 回カウントした測定のゆらぎは √N 回 である」
つまり、測定した「全計数値」とその「ゆらぎ」をセットで表すと、 N ± √N となります。（※この時点で選択肢1は、「計数率」ではなく「計数値」の話なので誤りと分かります）
✔ 最重要ポイント：「計数率」への誤差の伝播
次に、私たちが知りたい計数率（1秒あたりのカウント数）を求めます。 計数率は、全計数値を時間で割って算出します。
計数率 (R)= 全計数値 (N) / 測定時間 (t)
ここで、最も重要なポイントです。 「計数値」を「計数率」にするために時間 t で割ったのですから、その「ゆらぎ √N」も、同じ t で割ってあげなければ、単位が合いません。
- 計数率： N / t
- 計数率のゆらぎ： √N / t
✔ 結論：2つを合体させる
したがって、「計数率」とその「ゆらぎ（標準偏差）」をセットで表すと、選択肢4が正解となります。
出題者の“声”
この問題は、数式を見ただけで思考停止してしまう者をふるいにかける、典型的な問題じゃ。
しかし、本質は非常にシンプル。「放射線計測の“ゆらぎ”の基本ルール √N を知っているか」、そして「計数率（N/t）を求めるとき、誤差 √N もちゃんと t で割ったか」という、論理の正確さを問うておる。
3番を選んでしまった者は、最も典型的なワナにはまっておる。単位の違うもの同士は、足したり引いたりできない。これは物理学以前の、算数の大原則じゃ。
「カウント数/秒」と「カウント数」を平気で足し引きする答案は、放射線測定の基本を理解していないと即座に判断されるぞ。
臨床の“目”で読む
ーなぜ √N（ゆらぎ）を知ることが重要なのか？ー
この「√N」という統計的なゆらぎは、私たちが扱う放射線測定値が「本物か、誤差か」を判断するためのものさしになるからです。
- 汚染検査での判断
- サーベイメータである場所のバックグラウンド（BG）を測定したら、100カウントだったとします。
- √N のルールから、このBGのゆらぎは √100 = 10 カウント程度あると分かります。つまり、何もなくても90〜110カウント程度は普通に測定されうる、ということです。
- 次に、汚染が疑われる場所を測って115カウントだったら？
- BGとの差は15カウントですが、ゆらぎが10カウントあることを考えると、これは「誤差の範囲内かもしれない」と判断できます。
- しかし、もし150カウントだったら？
- 差は50カウントあり、ゆらぎの10カウントより遥かに大きいため、これは「誤差ではなく、有意な汚染がある」と断定できます。
- 装置の安定性確認（QA）
- 毎日行う核医学装置の感度チェック（デイリーチェック）で、√N の範囲を大きく超える変動が続くようであれば、装置の故障を疑うきっかけになります。
今日のまとめ
- 放射線の「計数値」には、統計的なゆらぎ（標準偏差）が常にあり、その大きさは √N である。
- 「計数率」とそのゆらぎを求めるには、両方を測定時間 t で割る。
- このゆらぎの大きさは、臨床現場で測定値が「誤差」なのか「意味のある変化」なのかを判断する基準となる。
コメント